|
``Zero-padding'' means adding additional zeros to a sample of data (after the data has been windowed, if applicable). For example, you may have 1023 data points, but you might want to run a 1024 point FFT or even a 2048 point FFT. There are two reasons why you might do this. First, from section6.1 we recall that the FFT is slow for prime numbers, but much faster for powers of two. We can add an extra zero to the end of the sample and thus get much better performance. On a modern PC, one need not be too concerned with this for moderate sample sizes. 1023 is not noticeably slower than 1024. But if one is running very big FFTs (100,000 or more) or using lower powered embedded devices, one might be concerned about this.
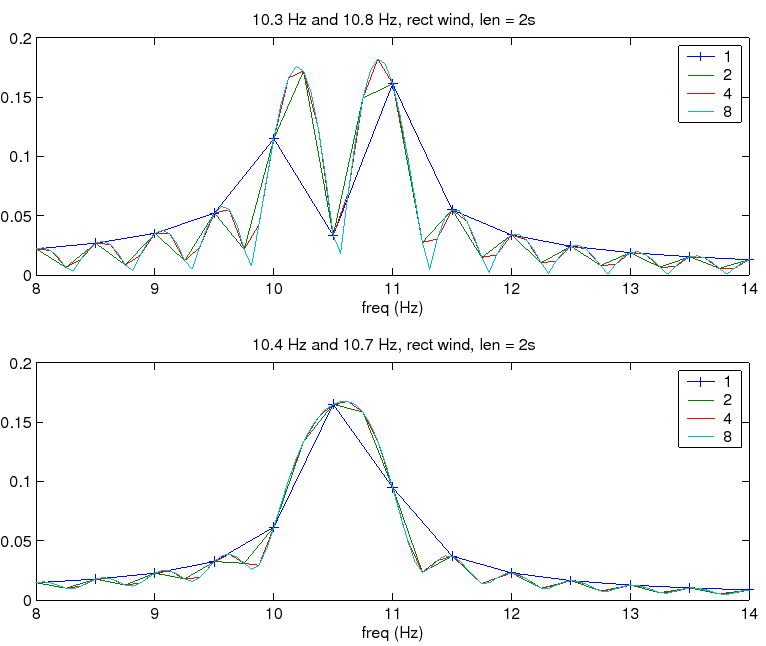
The other reason that zero-padding is used is to get better frequency resolution. There is something to be gained here, but it is very subtle. National Instruments has a good writeup on this [4]. Here is a summary. Recall from section 6.1 that the DFT is a sampling of the DTFT. Zero padding allows us to take more samples of the DTFT. For example, if we have 1000 points of data, sampled at 1000 Hz, and perform the standard FFT, I get a frequency bin every 1 Hz. But if I pad with 1000 zeros and then run a 2000 point FFT, now I get frequency bins every 0.5 Hz. This allows us to get around some of the disadvantages of the DFT (e.g. it may allow us to read amplitudes more accurately - reducing the spacing between bins may put a bin closer to true frequency of a signal and those avoid the picket fence effect). But, since all this does is sample the DTFT more finely, we cannot get around any inherent limitations of the DTFT itself. Most noteable, if your choice of window type and length do not allow you to resolve two closely spaced frequency components, then zero padding is not going to help. See fig:Zero-padding-ex.
Note that simply increasing the sampling rate does not confer the same benefits that zero padding does. What matters is the length of the data in seconds, not the length of the data in samples.
As mentioned at the begining of the section, if the data is to be windowed (which it probably should be), then the zero pad should be applied after the window. This is illustrated in Figure 15, where the signal is an 11 Hz sine wave. When taken with a 2 Hz resolution FFT and no window, there is significant leakage and picket fence effect. Adding a window reduces the leakage, but not the picket fence effect. Zero padding before the window doubles the frequency resolution to 1 Hz, and thus reduces the picket fence, but now the leakge has returned. The best procedure is to window first, then zero pad. The reason, of course, is that the point of the window is to smooth out the begining and end of the data sample. If the zero pad is applied first, then the middle of the data set could still be non-smooth.

|
